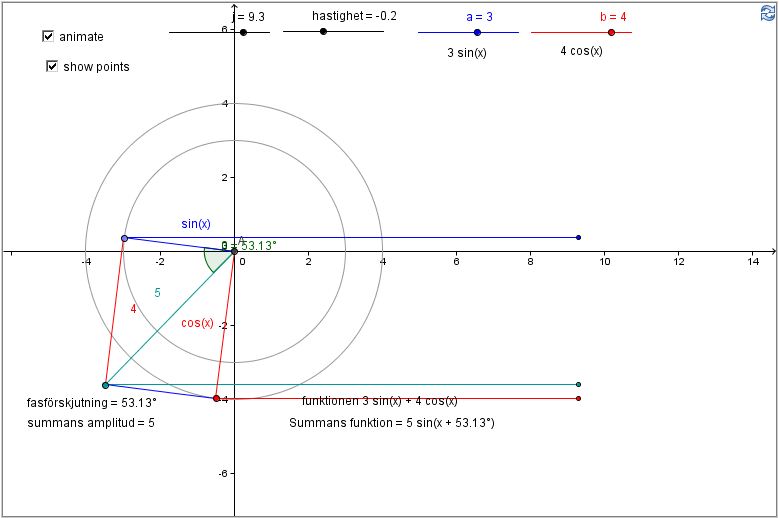
Série Fourier: Fazendo ondas
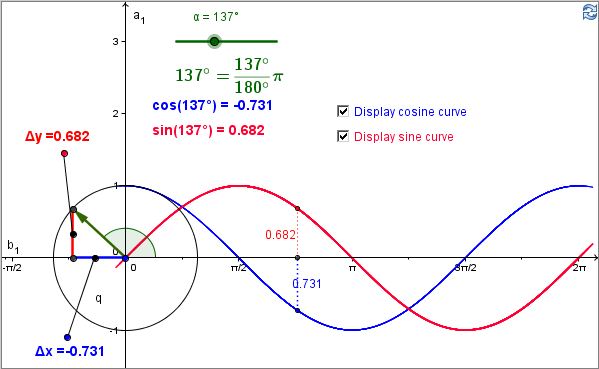
Veja como os senos e os cossenos se somam para produzir funções periódicas arbitrárias.
Descreva sons em termos de ondas sinusoidais. Compare e contraste ondas no espaço e ondas no tempo; Reconheça que o comprimento de onda e o período não correspondem a pontos específicos no gráfico, mas indicam o comprimento / tempo entre duas valas consecutivas, picos ou quaisquer outros pontos correspondentes;
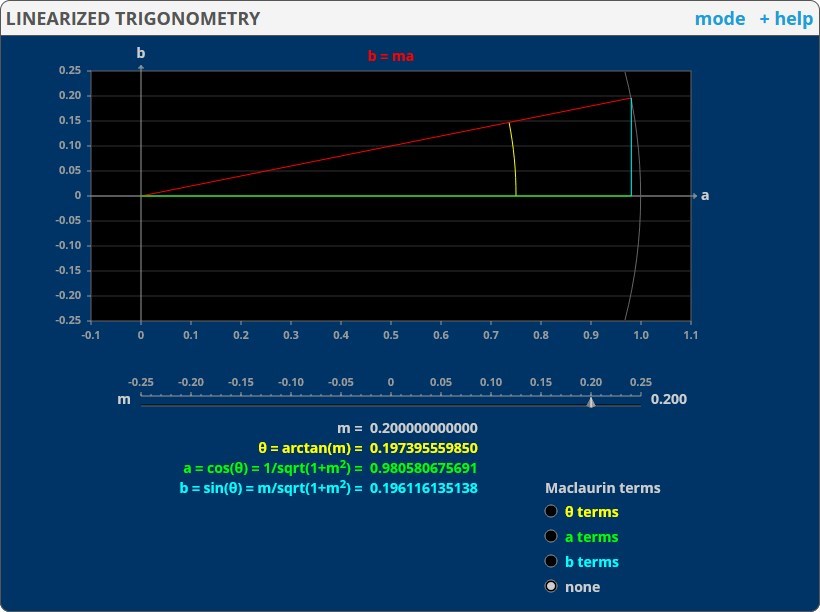
Relacione a notação matemática de uma série de Fourier à sua representação gráfica e determine qual aspecto do gráfico é descrito por cada um dos símbolos na equação;
Traduza uma equação da notação de somação para a notação expandida;
Reconheça que a largura de um pacote de ondas no espaço de posição está inversamente relacionada à largura de um pacote de ondas no espaço de Fourier;
Explique como o Princípio da Incerteza de Heisenberg resulta das propriedades das ondas;
Reconheça que o espaçamento entre os componentes de Fourier está inversamente relacionado ao espaçamento entre pacotes de ondas e que uma distribuição contínua dos componentes de Fourier leva a um único pacote de ondas.